Après avoir présenté, au chapitre précédent, les principales théories concernant l’évolution des langues, nous nous proposons maintenant d’élaborer un premier modèle linguistique assez général qui devra mettre en évidence les différents problèmes qui se posent en vue d’une implémentation sur l’ordinateur. Nous distinguerons entre un modèle idéal qui est censé être aussi près de l’évolution réelle que possible et un modèle pratique qui contient certaines simplifications.
Toutes les théories présentées jusqu’ici ont essayé de révéler les mécanismes responsables des changements phonétiques. Ces mécanismes étaient censés expliquer des faits réels et ils étaient dès lors considérés comme des « vérités linguistiques ». Les chercheurs ne se limitaient pas à « décrire », mais il se proposaient de découvrir les véritables « causes » de ces changements : ainsi, tel mot aurait été substitué par tel autre parce que, à un moment donné de l’évolution, il y aurait eu un conflit homonymique ; ou telle consonne sourde serait devenue sonore parce qu’elle se trouvait entre deux voyelles et qu’elle aurait donc subi une assimilation.
Lorsqu’on se propose de simuler (notons bien ce mot) des changements phonétiques sur un ordinateur, les choses se présentent de manière un peu différente : les évolutions calculées ne seront pas considérées comme des faits réels, mais comme des simples représentations de faits réels. Une simulation est donc moins « explicative » que « descriptive ». C’est ce que Hartmann dira de manière très claire dans l’introduction à son programme(1) : « PHONO and models testable by it make no claim as to whether rules "describe", "explain", "cause", "reflect", or merely "correspond to" actual sound changes ». Lorsqu’un t intervocalique passe donc à un d, l’ordinateur ne dira rien sur le pourquoi de ce changement : qu’il soit dû à une assimilation ou à un autre phénomène linguistique n’a pour lui pas la moindre importance. Il se contentera de vérifier que le t soit entouré de deux voyelles (ce qui correspond à la condition qui doit être remplie pour que la transformation puisse se produire) et substituera ensuite d à t.
Toute simulation est basée sur un modèle dont le but est de représenter de manière schématisée des faits réels. D’un point de vu abstrait, un modèle se compose de trois éléments essentiels : les faits (ou données), les relations (ou structures) et les opérations (ou transformations). Tous les trois sont intimement liés les uns aux autres : un fait considéré en dehors des relations qu’il maintient avec d’autres faits n’a donc (par définition) aucune valeur déterminée. De même, une opération ne peut effectuer aucune transformation sur les faits si elle ne tient pas compte des structures de ceux-ci. Afin de pouvoir mieux illustrer ce que nous entendons par « modèle », nous pourrions prendre l’exemple d’un jeu de billard : celui-ci se compose de faits (une série de boules numérotées) arrangés dans une certaine structure (une table où chaque boule a une place bien déterminée) et sur lesquels s’effectuent des opérations (les coups de queues des deux joueurs)(2).
Quant aux opérations, elles transforment typiquement un état A (appelé input) en un état B (appelé output). On peut distinguer entre des opérations simples, responsables de ce qu’on pourrait appeler des « transformation minimales », et des opérations complexes qui sont construites à partir des opérations simples, le procédé le plus fréquent étant celui d’enchaîner les opérations de sorte que l’output de l’une devient l’input de la suivante. Dans un jeu de billard, une opération simple serait par exemple un coup de queue donné par un des deux joueurs : au cours de celle-ci, une certaine disposition des boules (celle avant le coup) est transformée en une nouvelle disposition des boules après le coup. Une suite de plusieurs coups pourrait être considérée comme une opération complexe.
D’un point de vu conceptuel, un jeu de billard ne diffère en rien d’un modèle étymologique et si nous voulions les comparer nous pourrions dire que les boules correspondent aux mots que nous calculons, les coups de queue aux règles linguistiques et la table à un espace de calcul où il existe des bandes symboliques tout à fait analogues à celles – physiques – d’une table de billard. Nous n’en donnons qu’un exemple, la transformation d’un phonème sonore (d) en un phonème sourd (t).
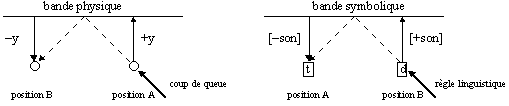
De même que la bande physique du billard répond au coup de queue en transformant le mouvement +y en –y, celle symbolique du modèle étymologique peut intervenir pour transformer le trait [+son] en [–son].
Il est clair que le modèle étymologique ne pourra être aussi simple que nous venons de le peindre et cela est dû surtout au grand nombre de faits qu’il doit être susceptible d’intégrer : le calcul peut en effet dépendre d’une grande quantité de facteurs parmi lesquels nous pouvons mentionner la structure phonologique du mot, le temps, mais aussi toute une série de variables qui semblent assez difficiles à cerner, tels que des facteurs grammaticaux, sémantiques, lexicaux, syntaxiques, etc. À ces faits correspondent autant de structures différentes : ainsi, la variable de temps ne pourra pas être traitée de la même façon que la structure phonologique du mot. Tandis que ces deux variables présentent des structures qui sont encore relativement faciles à déterminer (un axe temporel et un système phonologique), les derniers facteurs cités semblent plus difficiles : comment tenir compte des paradigmes grammaticaux, des rapprochements lexicaux entre les mots, des effets prosodiques dus à la syntaxe ? Ces structures sont, de plus, susceptibles de varier selon les langues (le latin, par exemple, n’a pas les mêmes catégories grammaticales que le français moderne). Il conviendrait donc d’avoir des structures suffisamment génériques pour s’adapter à différents types d’informations.
Après avoir introduit les termes « données », « structure » et « opération », nous pouvons dès maintenant répondre à une des questions fondamentales concernant le programme, à savoir quels phénomènes linguistiques sont théoriquement susceptibles d’être simulés par un ordinateur. La réponse est simple : en partant du principe qu’un ordinateur ne peut qu’être rigoureusement logique (ou mécanique, si l’on préfère) on peut dire que tout phénomène conforme aux deux règles suivantes peut, en théorie, être simulé :
Le phénomène doit être régulier, ou – formulé d’une manière un peu moins exigeante – plus un phénomène est régulier, plus les résultats de la simulation pourront correspondre aux faits réels. On pourrait parler, ici, d’une restriction extérieure (scientifique) qui n’a donc rien à voir avec le modèle.
Le phénomène doit être représentable à l’intérieur du modèle, ce qui veut dire que celui-ci doit offrir les données, les structures et les opérations qui sont nécessaires pour tenir compte de tous les aspects impliqués dans la transformation. Il s’agit ici d’une restriction intérieure (technique) qui dépend directement de l’efficacité du modèle.
Lorsqu’on se propose de développer un programme qui serve d’outil linguistique, on a donc intérêt à réduire les restrictions intérieures à un minimum. De cette façon, l’ordinateur devient un instrument idéal pour déterminer la régularité ou l’irrégularité des transformations linguistiques.
Après ces considérations d’ordre général, nous pouvons maintenant présenter un premier modèle concret de l’évolution linguistique. Ce modèle est basé sur la théorie ensembliste telle qu’on l’utilise en mathématiques. Il considère les langues comme des ensembles d’unités lexicales qui subissent des changements :

Nous avons, d’une part, une « langue de départ » (L1) contenant un certain nombre (n Î Ð) d’éléments lexicaux (m1, m2, ..., mn) et, d’autre part, un ensemble ordonné d’opérations ou, comme nous préférons les nommer, de règles (r1, r2, ..., ri-1, i Î Ð). Chaque règle rx crée un nouvel ensemble Lx+1 à partir d’un ensemble Lx existant (0 < x < i, x Î Ð) en transformant un certain nombre (0 < t £ n, t Î Ð) d’éléments m Î Lx (ce qui sous-entend, en même temps, que n–t éléments sont laissés intacts).
En termes mathématiques, nous pouvons considérer les règles comme des fonctions qui, appliquées de manière ordonnée les unes après les autres, constituent une fonction principale F :

Théoriquement, nous pourrions donc dire pour n’importe quel élément mx Î L1 (0 < x £ n, x Î Ð) que mx* = F(mx) est son élément correspondant dans Li. Mais les choses ne sont, évidemment, pas aussi simples que cela.
Lorsque nous considérons, par exemple, les deux mots latins EQUAM et EQUUM, nous constatons que l’un a donné yegua « jument » en espagnol, tandis que l’autre n’a pas laissé de traces. Cela veut dire qu’il n’existe pas de y Î Li de sorte que F(x) (!)=(!) y. Nous devons donc conclure que la fonction F(x) n’est pas définie pour certains éléments x Î L1 (3). Schématiquement, ce cas se présente de la façon suivante :

De même, il est possible que, dans la langue réelle – disons Lr – que l’ensemble Li est censé représenter, il existe des éléments qui ne font pas partie de Li. Mathématiquement parlant : (x Î Lr) Ù (x Ï Li) Ù (Li Ì Lr) :

D’un point de vue linguistique, ces mots peuvent être considérés comme des néologismes, des dérivations (formation d’un nouveau mot à partir d’une racine et d’un suffixe qui existent déjà dans la langue), des mots d’emprunt, etc.
Le modèle tel que nous venons de le présenter sous-entend, en principe, que chaque règle s’applique simultanément à tous les mots, c’est-à-dire que tous les éléments (m1, m2, ..., mn) sont calculés en parallèle. Même si, du point de vue théorique, les choses se sont sûrement passées de la sorte, il est évident qu’à cause du nombre assez élevé de mots qui existent dans une langue, même un ordinateur puissant risque de ne pas disposer de suffisamment de mémoire pour représenter toutes ces données.
Pour un ordinateur, il est donc préférable que les évolutions soient calculées de manière individuelle. Ceci est en effet possible encore que cette réduction ne reste pas sans conséquences pour le nombre de phénomènes qui pourront être simulés. Il est par exemple évident que, dans ce cas, les conflits homonymiques ou les analogies (qui constituent des espèces de phénomènes « transversaux », par opposition aux évolutions « linéaires » décrites par les règles phonétiques) ne pourront pas être calculés.
Jusqu’à maintenant, nous sommes partis du principe que les transformations décrites par les règles étaient univoques dans le sens où elles ne peuvent donner lieu qu’à une seule ligne évolutive. Cela n’est pourtant pas le cas, comme le montrent les deux exemples latins DOMINUM et HOMINEM qui ont donné dueño et hombre en espagnol : le phénomène le plus remarquable dans l’évolution de ces mots, consiste dans le fait qu’après la syncope du i, le groupe consonantique m’n a évolué de deux façons différentes(4) :
DOMINU(M) > dom’nu > dom’no > duem’no > duenno > dueño
HOMINE(M) > hom’ne > hom’re > hombre
Dans le premier cas, le groupe subit une assimilation et se palatalise ensuite. Dans le deuxième, il subit au contraire une dissimilation, ce qui conduit à l’insertion d’une consonne épenthétique b. Afin que les deux évolutions puissent être poursuivies, le programme doit permettre d’utiliser des règles qui décrivent plusieurs évolutions possibles (c’est ce que nous appellerons par la suite des « évolutions multiples »). Notons que dans notre exemple, il y a encore une deuxième ambiguïté à résoudre : les deux mots contiennent un o ouvert tonique qui, en général, se diphtongue en espagnol (pour donner [wé]). Mais lorsque la voyelle se trouve devant une consonne nasale, il y a de nouveau deux évolutions possibles : soit le o se diphtongue, soit il passe à o fermé. En tout, nous avons donc quatre évolutions possibles :
Pour DOMINU(M)

Pour HOMINE(M)

Nous voyons que les deux solutions correctes sont diamétralement opposées. En effet, rien ne nous permet de savoir à l’avance quelle évolution sera choisie par le mot, de sorte qu’il est nécessaire de tenir compte de toutes les évolutions possibles si nous ne voulons pas omettre la correcte.
La bifurcation des évolutions peut paraître problématique, puisqu’on aboutit à un nombre assez élevé d’évolutions que l’ordinateur doit gérer. Le nombre exact des bifurcations après n règles peut être calculé à l’aide de la formule récursive

où e(n) est le nombre des évolutions possibles de la n-ième règle et b(n) la somme de toutes les évolutions possibles jusqu’à la n-ième règle. Comme seules les règles avec e(n) > 1 augmentent le nombre des évolutions, on peut dire que le nombre des règles est indifférent. Dans un ensemble hypothétique de n règles, on peut donc dire que s’il y a m règles avec au moins deux évolutions possibles, le nombre maximal des évolutions est > 2(m) (si toutes les règles à deux évolutions sont appliquées). La croissance du nombre des évolutions est donc exponentielle, ce qui risque de poser des problèmes dans la gestion de ces dernières par l’ordinateur, problème que nous rencontrerons encore à plusieurs reprises dans les prochains chapitres.
Les lois phonétiques n’agissent que pendant un certain temps de sorte qu’il est nécessaire d’intégrer cette variable dans le calcul. A première vue, cette tâche semble simple : en supposant qu’il doit être possible de déterminer, pour chaque loi phonétique le moment précis où elle a provoqué le changement, le seul travail à faire consisterait à mettre les règles dans un ordre chronologique (séquentiel). Chaque ensemble Lx (1 < x £ i) constituerait donc une « tranche de temps » synchronique dont la date correspondrait à celle de la règle qui l’a produite.
Mais, une fois de plus, les choses ne sont pas aussi simples : il est souvent difficile de déterminer le moment exact d’une loi phonétique puisque celles-ci s’étendent sur un espace plus ou moins long sur l’axe temporel. À cause d’une simultanéité partielle, certaines lois peuvent se « chevaucher ». En d’autres termes, il est possible que plusieurs lois phonétiques entrent en compétition entre elles. Dans de tels cas, leur ordre d’application est souvent imprévisible et peut différer de mot en mot. Prenons les deux exemples lat. SOLITUM > esp. sueldo et lat. SOLUTUM > esp. suelto. Tandis que, dans le premier, la sonorisation a lieu avant la syncope, elle ne se produit pas dans le deuxième où la syncope, de toute évidence, est antérieure(5).
Une possibilité relativement facile de tenir compte de ces chevauchements peut être celle d’admettre des « évolutions multiples ». Dans l’exemple discuté, nous pourrions donc formuler une règle qui dirait que lorsque une consonne intervocalique se situe après une voyelle atone interne (qui est susceptible de tomber) celle-ci peut ou non se sonoriser. Grâce à ce petit artifice il est effectivement possible de simuler la simultanéité de certaines lois phonétiques tout en conservant l’ordre séquentiel des règles ce qui simplifie le calcul.
A l’intérieur du lexique d’une langue, on distingue, en général, entre les mots populaires, qui ont été transmis par une tradition orale ininterrompue(6), et les cultismes qui, empruntés à une autre langue, n’ont pas suivi cette évolution (exception faite de quelques petites modifications qui peuvent se produire dans les terminaisons(7)) et qui sont donc restés « tels quels ». On distingue, outre cela, les sémi-cultismes qui sont considérés comme des espèces d’« hybrides » dans le sens où ils participent à certains changements populaires tout en restant indifférents à d’autres(8).
Afin de pouvoir réfléchir de manière systématique sur les cultismes et les sémi-cultismes, nous commençons par admettre deux hypothèses : (1) nous considérons qu’il n’y a pas de vraie différence entre les cultismes et les sémi-cultismes étant donné que les deux se caractérisent essentiellement par une non-participation – qu’elle soit partielle ou totale – à l’évolution populaire, et (2) nous supposons qu’il existe pour tout (sémi-)cultisme un moment x à partir duquel il suit l’évolution phonétique régulière (au même titre que les mots populaires)(9). Nous supposons, en d’autres termes, que tout (sémi-)cultisme se transformera, tôt ou tard, en mot populaire et subira, à partir de là, tous les changements phonétiques de ceux-ci.
En partant de ces deux hypothèses, nous devons d’abord nous demander à quel moment exactement les (sémi-)cultismes « entrent » dans la langue ou plutôt, formulé dans l’optique de notre modèle, à quel moment ils entrent dans la chaîne du calcul (constituée par les règles r1, r2, ... ri). On peut s’imaginer deux scénarios : soit (1) les cultismes suivent le calcul dès le début (et dans ce cas ils existent parallèlement aux mots populaires sans pourtant subir les évolutions phonétiques de ceux-ci), soit (2) ils y entrent plus tard (par exemple au moment où ils commencent à participer à l’évolution phonétique des mots populaires).

Dans le premier cas, vu que tant les mots populaires que les (sémi-)cultismes font partie du calcul, les règles r1, r2, ..., rx-1 doivent forcément décrire deux évolutions possibles : (1) l’évolution des mots populaires et (2) la non-évolution (ou évolution « zéro ») des (sémi-)cultismes. Dans le deuxième cas, les règles r1, r2, ..., rx-1 ne décriraient qu’une seule évolution, à savoir celle des mots populaires. La non-évolution des cultismes serait donc simulée par la non-application des règles r1, r2, ..., rx-1.
Si nous optons pour le premier type de calcul, nous ne pourrons éviter de produire un grand nombre d’évolutions (problème auquel nous avons déjà fait allusion et qui se présente ici sous forme aggravée) : étant donné que chaque règle pourrait avoir au moins deux évolutions (celle populaire et celle savante), le nombre d’évolutions théoriquement possibles s’élèverait à au moins 2(n) possibilités pour n règles. Il est certes vrai que certaines possibilités peuvent être exclues par avance (ainsi, la règle qui décrit l’assourdissement du s intervocalique en espagnol moderne semble s’appliquer dans tous les cas, même dans le cultismes, de sorte qu’il ne serait pas nécessaire de faire bifurquer la ligne du calcul), mais même en soustrayant ces cas, il reste un nombre très élevé de possibilités. Nous pourrions aussi penser à trouver des critères qui permettent de déterminer si un mot est un cultisme ou non (ce qui simplifierait donc au moins le calcul des mots populaires), mais cela est évidemment tout sauf un problème trivial(10). Il semble donc indispensable d’opter pour le deuxième type de calcul et de simuler la non-évolution des (sémi-)cultismes par la non-application de certaines règles.
Nous étions partis de l’hypothèse qu’à partir d’un certain moment x, tout (sémi-)cultisme devient un mot populaire de telle sorte qu’il suit une évolution phonétique régulière. Il se trouve que cette hypothèse est elle aussi fausse (ou qu’elle n’est, au moins, pas entièrement correcte). Si nous prenons, par exemple, l’évolution du mot latin CLERICUM qui a donné clérigo en espagnol, nous constatons que ce mot présente à la fois des traits populaires (perte du m final, ouverture de la voyelle finale, sonorisation du k intervocalique) et des traits savants (il n’y a pas de syncope, le groupe initial kl aurait dû aboutir à ll (par palatalisation) ; si le mot avait suivi toute l’évolution populaire, le résultat serait probablement *llergo). Ce qui est curieux, c’est que du point de vue chronologique, la sonorisation du k intervocalique est probablement antérieure à la palatalisation du groupe initial kl(11). Nous avons donc à faire à un mot qui, au début, se comporte comme un mot populaire pour se rapprocher ensuite des cultismes.
Face à ce dilemme, que faire ? Tout d’abord, il semble, en effet, que nous devons définitivement abandonner notre deuxième hypothèse : un (sémi-)cultisme, même s’il participe à un changement x, n’a aucune raison de participer à un autre changement y postérieur à x. Nous pourrions même être tentés de conclure que tout changement linguistique – indépendamment du moment où il se produit – est forcément ambigu dans le sens où il peut ou non se produire. S’il en était ainsi, la grande question que l’on devrait se poser est celle de savoir comment on peut simuler cet état de faits. Une première possibilité, insatisfaisante comme nous l’avons déjà dit, puisqu’elle mène à une croissance exponentielle des évolutions à calculer, consiste à admettre des règles qui décrivent, à chaque fois, deux évolutions possibles (celle populaire et celle savante). Une autre possibilité consisterait peut-être à abandonner l’idée de la séquentialité des règles : il faudrait alors élaborer un modèle complètement différent qui permette de mieux tenir compte de l’extension temporelle des lois phonétiques (et par là des « chevauchements » possibles entre elles). Il faudrait se demander, dans ce cas, s’il n’existe pas différents types de lois phonétiques(12).
Ces considérations ont montré que le problème des (sémi-)cultismes est tout sauf trivial, et il semble, en effet, qu’il ne peut pas être résolu pour l’instant. Car même si nous savons que leur calcul sera toujours déficient dans un modèle de règles séquentielles, aucune autre approche ne semble s’offrir pour le moment.
Si l’intégration de la variable temporelle s’est déjà avérée quelque peu difficile (nous avons soulevé, notamment, les problèmes en rapport avec la séquentialité des règles), la dimension spatiale semble encore plus complexe. Il se trouve que l’évolution d’une langue ne dépend pas seulement des lois phonétiques – et de l’extension géographique de celles-ci –, mais aussi de ce que nous appellerons des « phénomènes de migration » : par ce terme, nous nous référons à ce qu’une langue peut, au cours du temps, amplifier ou réduire le territoire géographique qu’elle occupe. Le latin, par exemple, n’était, au début, qu’un dialecte parmi d’autres qui était parlé dans une petite région appelée LATIUM. Petit à petit, ce dialecte a commencé à gagner du terrain et s’est finalement répandu sur le territoire que nous nommons aujourd’hui la ROMANIA.
Si nous voulons tenir compte des phénomènes spatiaux, nous sommes donc obligés d’introduire un nouveau type de règles que nous appellerons des « règles de migration ». Celles-ci décrivent la propagation d’une langue – plus précisément de ses éléments lexicaux – dans l’espace géographique :

Nous avons donc un espace géographique (G) dont une certaine partie (E1) est, à un moment donné (ici désigné par 1), occupée par une langue qui, à la suite d’une migration (décrite par la règle rm), s’étend (à un moment 2) sur un espace plus grand (E2). Dans cet exemple, l’extension E1 fait partie de l’extension E2, mais cela n’est pas forcément nécessaire.
Nous avons maintenant envisagé le problème du point de vue de la migration. Il ne faut pas oublier, cependant, que les lois phonétiques ont elles aussi une extension géographique bien déterminée. Ces deux problèmes – extension du lexique et extension des lois phonétiques – sont intimement liés et ne peuvent être traités indépendamment. Imaginons, par exemple, le cas suivant : nous avons une langue qui, à un moment donné, a une extension lexicale E1 et qui s’étend ensuite sur un territoire plus grand que nous appelons E2 (extension qui est décrite par la règle de migration rm). Une fois que cette expansion est terminée, une loi phonétique affecte une partie de E2 de telle sorte qu’elle touche à la fois des régions de l’ancienne zone (E1) et de la zone nouvellement conquise (E2 \ E1) :
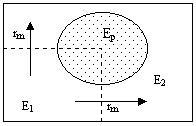
On peut maintenant inverser la perspective et dire que ce n’est pas la loi phonétique qui affecte une certaine partie de la distribution des éléments lexicaux, mais que, au contraire, ce sont les éléments lexicaux qui s’étendent sur des zones qui, plus tard, seront affectées par des lois phonétiques. Schématiquement :

Avec :
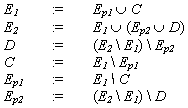
L’extension de la loi phonétique se définit donc comme Ep = Ep1 È Ep2. On aura remarqué que les définitions sont circulaires ce qui veut dire que le linguiste doit d’abord, à l’aide d’une recherche empirique, déterminer les limites à la fois de l’extension lexicale à différents moments historiques (ce qui correspond à E1 et E2) et celle de l’extension phonétique (Ep) afin de pouvoir en déduire les zones C, D, Ep1 et Ep2.
La deuxième perspective semble plus efficace dans la mesure où elle permet à la fois de décrire la migration et de déterminer exactement quelles zones de E1 et E2 ont été affectées par la loi phonétique :

Ainsi, chaque zone (C, D, Ep1, Ep2) décrit une région linguistique à la fois homogène et potentiellement différente(13).
Dans un des chapitres précédents, nous avons montré que DOMINUM et HOMINEM peuvent avoir au moins quatre évolutions possibles. Nous avons dit que cette ambiguïté dans l’évolution était due à la non-univocité de la loi phonétique. Quoique cette explication semble assez crédible, on pourrait aussi s’imaginer d’autres processus qui aboutiraient au même résultat. On peut s’imaginer, par exemple, que deux mots qui présentent des contextes phonétiques identiques (ou similaires) évoluent de manière différente dû au fait que cette évolution a lieu dans deux endroits différents (par exemple deux zones dialectales voisines qui ne subissent pas les mêmes changements phonétiques). Il se peut qu’un des deux mots soit ensuite transféré dans l’autre et que, une fois installé dans le dialecte voisin, ne soit plus reconnu comme un emprunt. En oubliant qu’il y a eu un phénomène de migration, on pourrait donc avoir l’impression que les contextes phonétiques identiques ont évolué de deux manières différentes à l’intérieur de la même zone. Schématiquement, ce cas se présente comme suit :

La différence dans l’évolution s’explique donc ici par une combinaison de deux règles phonétiques différentes (pa et pb) et d’une règle de migration (rm). Notons que Charles L. Eastlack mentionne cette possibilité pour hembra et dueña(14).
Nous avons vu que l’espace peut être intégré dans le modèle à l’aide d’intersections spatiales qui peuvent se produire entre les extensions des différentes migrations, entre les extensions des différentes lois phonétiques ou, finalement, entre les deux types d’extensions. Vu les nombreuses possibilités qui existent pour que des intersections se produisent, on peut se demander à combien d’intersections on doit théoriquement s’attendre. Du point de vue mathématique, le problème est vite résolu : lorsqu’on a un ensemble de base (disons B) et un certain nombre (n) de sous-ensembles par rapport à l’ensemble de base, il existe, en principe, 2(n) combinaisons possibles. À nouveau, nous avons donc affaire à une variable qui augmente de manière exponentielle le nombre des évolutions que l’ordinateur doit gérer.
Face au grand nombre de zones géographiques différentes, nous avons intérêt à trouver une solution qui permette de minimiser l’effort de calcul. Une telle solution s’offre effectivement : au lieu de calculer toutes les zones simultanément, on peut se limiter à une seule zone. Outre cela, on peut laisser de côté l’aspect de la migration. Un schéma peut illustrer cette approche simplifiée du problème :
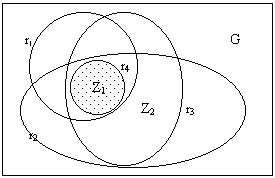
Nous avons donc un espace géographique (G) et quatre lois phonétiques (r1, r2, r3, r4) avec des extensions géographiques différentes. Au lieu de calculer toutes les zones, on peut se limiter à une zone particulière, par exemple Z1 ou Z2. Suivant la région que l’on choisit, l’ensemble de règles qui s’applique aux mots est différent : dans le cas de Z1, toutes les règles entrent en jeu, tandis que dans celui de Z2, seuls r2 et r3 s’appliquent.
Lorsqu’on ne calcule qu’une seule zone, le problème de la migration devient inexistant : il faut tout simplement déterminer le moment où la zone a été envahie par la langue(15) et, à partir de là, appliquer toutes les règles postérieures.
Jusqu’à maintenant, nous sommes partis du principe que nous calculerions la langue moderne à partir de la langue ancienne. On peut se demander, pourtant, si on ne peut pas inverser la direction du calcul, ce qui signifierait donc revenir à l’ancienne langue à partir de la langue moderne.
Nous avons considéré les règles comme des fonctions mathématiques qui, toutes ensemble, constituent une fonction principale :

Nous serions donc intéressés par la fonction inverse de F qui se définirait comme

La fonction principale F peut être inversée si (et uniquement si) toutes les sous-fonctions (règles) peuvent être inversées. En termes mathématiques, cela n’est possible que si les fonctions en question sont bijectives, c’est-à-dire à la fois injectives et surjectives. Or, il se trouve que nos fonctions ne sont ni l’un ni l’autre comme nous le montrent les contre-exemples suivants(16) :
| non-surjectivité : | nous pouvons citer modem, acronyme composé à partir des mots anglais modulator + demodulator. Ce mot n’a donc aucun antécédent, mais a été formé directement à partir de deux éléments de la langue moderne. |
| non-injectivité : | le mot français [so] auquel correspondent quatre graphies – saut, sot, sceau, seau – dont chacune provient d’un étimon latin différent, à savoir SALTUM (latin classique), SOTTUM (bas latin à partir du XIe siècle), SIGILLUM (latin classique), *SITELLUM (latin vulgaire, dérivé du latin classique SITULUM). |
Même si, en principe, la fonction F n’est pas bijective, on peut supposer qu’il existe, malgré tout, certaines possibilités d’inversion du fait que toutes les sous-fonctions ne sont pas aussi non bijectives que d’autres. Il faut admettre, cependant, que ces possibilités sont plutôt limitées : on constate, en général, une réduction considérable du matériel phonétique lorsqu’on passe de la langue ancienne à la langue moderne (cf. le mot latin AUGUSTUM – huit phonèmes – qui a donné août en français et qui, selon la prononciation que l’on adopte, s’est réduit à un [u] ou deux [ut] phonèmes). Tout compte fait, il semble donc plus facile de calculer de la langue ancienne à la langue moderne qu’à l’inverse. Dans ce dernier cas, la méthode historique-comparative semble nettement plus fructueuse.
Nous avons présenté toute une série de réflexions sur la manière dont l’évolution diachronique d’une langue peut – ou devrait – être simulée sur un ordinateur. Nous aimerions maintenant reprendre encore une fois tous ces éléments dans l’ensemble afin de pouvoir situer ensuite l’approche que nous avons choisi pour ETYMO. Voici donc un tableau synoptique des idées présentées :
|
|
modèle idéal |
modèle pratique |
|
Données et structures |
- données phonétiques avec une structure phonologique - système de traits distinctifs (phonologiques et autres) |
idem |
|
Opérations |
- implications logiques du type « SI x, alors y » - formalisme qui permette de tenir compte des évolutions multiples (cf. « SI x, ALORS y1 ou y2 ou ... ou yn ») |
idem |
|
Calcul du lexique |
- parallèle (simultané) - possibilité de simuler des conflits homonymiques (ou d’autres phénomènes « transversaux ») |
- individuel - seules les descendances « linéaires » peuvent être simulées |
|
Intégration du temps |
- ordre séquentiel des règles - evtl. un autre modèle avec différents types de règles (p. ex. règles locales vs règles universelles) |
idem |
|
Intégration de l’espace |
calcul simultané de plusieurs zones (= intersections entre les extensions des migrations et celles des lois phonétiques) |
- une seule zone est calculée - les règles s’organisent en fonction de la zone choisie - les phénomènes de migrations sont laissés de côté |
|
Types de règles |
- règles de migration - règles phonétiques |
règles phonétiques |
|
Evolutions non-univoques |
deux possibilités :
|
une seule possibilité : règle phonétique non univoque |
|
(Sémi-)cultismes |
deux possibilités :
=> aucune des deux solutions n’est satisfaisante |
idem |
Dans cette grille, ETYMO suit exactement le modèle pratique, ce qui veut dire qu’il est loin d’être un programme étymologique idéal. Néanmoins, nous le considérons comme une bonne base à partir de laquelle on peut étendre le modèle. Parmi les aspects non intégrés, la dimension spatiale est sans doute l’un des plus urgents. Le calcul individuel des mots, par contre, constitue un défaut de moindre importance.
1 Voir le fichier README.TXT (section 1.3) dans le répertoire PHONO sur le CD-ROM qui accompagne ce travail. Voir aussi le chapitre , p. et l’annexe.
2 Notons que cet exemple est extrêmement simplifié car la simulation d’un jeu de billard exige non seulement un modèle physique – qui est capable de calculer le mouvement des boules –, mais aussi des faits et des structures symboliques tels que la règle selon laquelle la boule noire ne peut pas être jouée au début d’une partie ou le fait qu’une boule appartient à l’un ou l’autre joueur.
3 Vu que F(x) est une fonction composée du type rn( rn-1( rn-2( ... r2( r1( x )) ... ))) on pourrait dire qu’au moins une des fonctions rj(x), 0 < j £ n, est non définie par rapport à x et que, par conséquent, toutes les fonctions subséquentes rk(x), j < k £ n, sont, elles aussi, non définies.
4 Nous ne donnons ici que les pas principaux de l’évolution.
5 Ces phénomènes sont considérablement complexes de sorte que nous ne pouvons en donner ici qu’une vision très réduite. Pour plus de détails, voir Carmen Pensado Ruiz, op. cit., 1984.
6 « Palabras populares o patrimoniales son aquellas que se han transmitido en una lengua determinada a través de un uso oral ininterrumpido ». C’est nous qui soulignons. Penny, op. cit., 1993, p. 34.
7 « Son palabras cultas aquellas que el español ha tomado en préstamo del latín (clásico o medieval), a través de la escritura. Tales préstamos, que eran ya frecuentes en la Edad Media, se han dado en todas las épocas y no han sufrido la evolución propia de las voces populares, sino apenas pequeñas modificaciones en sus terminaciones para ajustarse a las estructuras morfológicas del español ». Penny, op. cit., 1993, p. 34.
8 En effet, les définitions ne sont pas très claires et Ralph Penny le dit lui-même : « Ha habido una amplia controversia sobre la definición precisa del término semicultismo [..]. Catalogamos así las palabras que, aunque han sido heredadas oralmente del latín vulgar (en esto coinciden con las patrimoniales), han experimentado una remodelación, generalmente durante el período medieval, por influencia del latín, que era en esa época la lengua empleada en la iglesia, en los tribunales, etc. Debido a su transmisión oral, los semicultismos han conocido algunos de los cambios propios de las voces populares (pero no todos, por definición) ». Penny, op. cit., 1993, p. 34.
9 Hypothèse qui est évidemment fort douteuse, comme nous le montrerons par la suite.
10 Evidemment, on pourrait penser à la fréquence d’un mot ou alors au nombre de locuteurs qui l’utilisent (en tenant compte du fait que les cultismes sont, en général, des mots peu fréquents et qui sont utilisés par un nombre souvent assez restreint de locuteurs). Mais cette information, d’où provient-elle? Une bonne simulation calcule le passage d’un état A à un état B en ne recourant qu’aux éléments disponibles dans A. Or, la fréquence d’un mot, justement, peut changer au cours des siècles. Il faudrait donc trouver un critère dans A qui permette de prévoir la fréquence d’un mot pour n’importe quelle phase intermédiaire entre A et B. Même si nous supposions que cela fût théoriquement possible, une telle simulation dépasserait largement le domaine linguistique et devrait donc inclure des aspects beaucoup plus complexes.
11 Nous nous basons ici sur la liste de règles établie par Coloma Lleal, « Unos apuntes de fonética diacrónica ».
12 On pourrait distinguer, par exemple, entre des lois phonétiques « locales », limitées dans l’espace et dans le temps, et des lois phonétiques « universelles » qui seraient donc valables à n’importe quel moment et – peut-être aussi – à n’importe quel point géographique. Une telle loi universelle pourrait être, par exemple, la fusion de deux voyelles identiques, phénomène qui – au moins comme tendance – a été en vigueur à n’importe quel moment de l’évolution diachronique de l’espagnol. Nous devons impérativement mentionner, à cet endroit, le programme PHONO de Lee Hartmann qui distingue entre des « règles séquentielles » et des « règles persistantes ». Voir ch. , p. ).
13 Nous écrivons « potentiellement différent » parce que, dans l’exemple que nous avons décrit, les zones C et D ne seront probablement pas différentes du point de vue phonétique. Mais on peut sans problème s’imaginer des cas ou C et D seraient différents (il pourrait par exemple y avoir une loi phonétique qui n’affecte que C ou D).
14 Charles Eastlack, op. cit., 1977, p. 85.
15 Si toute la région n’a pas été colonisée en même temps, il faudrait alors la diviser en d’autres zones et calculer séparément chacune de celles-ci.
16 Voir aussi ch. , p. .
| Retour à la page principale | << Chapitre précédent | Chapitre suivant >> |